A B-Tree data structure is a self-balancing m-way tree that allows searches, insertions, and deletions to be performed in logarithmic times. Each node of a B Tree with order m may have m children and m-1 keys.
B-Tree is a generalization to binary search trees (BSTs). A BST sorts the data in a BST but unlike BSTs, a B Tree can have more than 2 child nodes.
children. This keeps the height of the B-Tree tree small. We will see later how having multiple keys in one node can help with data locality.
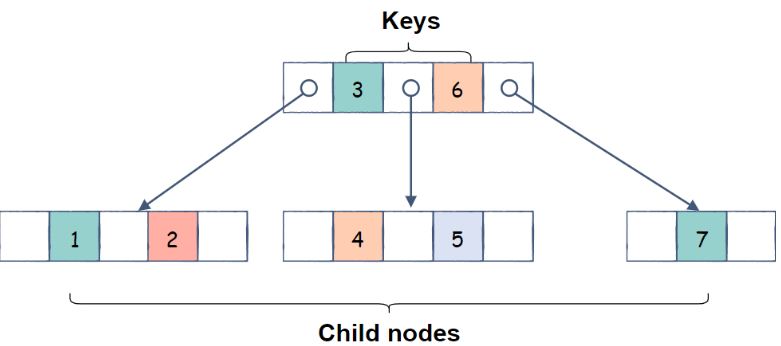
In summary, a B-Tree of the order m has the following properties:
- Each node has a maximum of m children
- A node with n child nodes must have n-1 keys
- All leaf nodes are at a similar level
- Every node except the root is at least half-filled
- If it is not a Leaf, the root has at least 2 children
Importance of B-Trees
B-trees are essential for optimizing data storage, retrieval, and other operations in a variety of applications, such as databases, file systems, and filesystems. Their balanced nature allows for efficient access and makes them indispensable in scenarios that require rapid data access.
B-Tree Structure
Nodes in a B-Tree
A B-Tree is made up of nodes that contain a variable number of keys and child pointers. These nodes are arranged hierarchically starting with the root node. Internal nodes contain pointers and keys to child nodes. Leaf nodes store data or pointers that point to data records.
B-Tree Operations
B-Trees are capable of various operations, including insertion, deletion, and searching. These operations are carefully designed to maintain the balance of the tree and ensure optimal performance, even with large datasets.
Binary Tree vs. B-Tree
The structure of a B Tree and a Binary Tree is one of the main differences. While a binary node can only have two children, a B Tree can have any number of child nodes. This ranges from two to hundreds.
Operations
Searching :
Searching in Binary Trees is the same as searching in B Trees. If we search for item 49 in this B Tree, the process will look like: The process will look like this:
- Compare item 49 to root node 78. Since 49 78, move the sub-tree to its left.
- If you have 404956, then traverse the right subtree.
- Compare 49.45. Move to the right. Compare 49.
- Return if you find a match
The height of a B-tree determines the time it takes to search for an element. The search algorithm requires O(log n).
Inserting
Insertions are made at the level of the leaf node. To insert an item in B Tree, you need to follow the following algorithm.
- To insert the node, traverse the B Tree to find the appropriate node.
- If the leaf node contains less than an m-1 key then insert the element in increasing order.
- If the leaf node contains keys m-1, then you should follow the steps below.
- Insert the new element into the increasing order.
- Divide the node in two at the median.
- Push the middle element up to its parent node.
- If the parent node contains m-1 keys, split it by following the same steps.
Example
Following are the implementations of this operation in various programming languages −
// C Program for B trees
#include <stdio.h>
#include <stdlib.h>
struct BTree {
//node declaration
int *d;
struct BTree **child_ptr;
int l;
int n;
};
struct BTree *r = NULL;
struct BTree *np = NULL;
struct BTree *x = NULL;
//creation of node
struct BTree* init() {
int i;
np = (struct BTree*)malloc(sizeof(struct BTree));
//order 6
np->d = (int*)malloc(6 * sizeof(int));
np->child_ptr = (struct BTree**)malloc(7 * sizeof(struct BTree*));
np->l = 1;
np->n = 0;
for (i = 0; i < 7; i++) {
np->child_ptr[i] = NULL;
}
return np;
}
//traverse the tree
void traverse(struct BTree *p) {
printf("\n");
int i;
for (i = 0; i < p->n; i++) {
if (p->l == 0) {
traverse(p->child_ptr[i]);
}
printf(" %d", p->d[i]);
}
if (p->l == 0) {
traverse(p->child_ptr[i]);
}
printf("\n");
}
//sort the tree
void sort(int *p, int n) {
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] > p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
int split_child(struct BTree *x, int i) {
int j, mid;
struct BTree *np1, *np3, *y;
np3 = init();
//create new node
np3->l = 1;
if (i == -1) {
mid = x->d[2];
//find mid
x->d[2] = 0;
x->n--;
np1 = init();
np1->l = 0;
x->l = 1;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = x->d[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->d[j] = 0;
x->n--;
}
for (j = 0; j < 6; j++) {
x->child_ptr[j] = NULL;
}
np1->d[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
r = np1;
} else {
y = x->child_ptr[i];
mid = y->d[2];
y->d[2] = 0;
y->n--;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = y->d[j];
np3->n++;
y->d[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insert(int a) {
int i, t;
x = r;
if (x == NULL) {
r = init();
x = r;
} else {
if (x->l == 1 && x->n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < x->n; i++) {
if (a > x->d[i] && a < x->d[i + 1]) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
x = x->child_ptr[i];
} else {
while (x->l == 0) {
for (i = 0; i < x->n; i++) {
if (a > x->d[i] && a < x->d[i + 1]) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
if (x->child_ptr[i]->n == 6) {
t = split_child(x, i);
x->d[x->n] = t;
x->n++;
continue;
} else {
x = x->child_ptr[i];
}
}
}
}
x->d[x->n] = a;
sort(x->d, x->n);
x->n++;
}
int main() {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
printf("Insertion Done");
printf("\nB tree:");
traverse(r);
Output
Insertion Done
BTree elements before deletion:
8 9 10 11 15 16 17 18 20 23
The element to be deleted: 20
BTree elements before deletion:
8 9 10 11 15 16 17 18 23 8 9 23
FAQs
- What is the maximum degree of a B-Tree?
The maximum degree of a B-Tree determines the maximum number of child pointers a node can have. It directly impacts the tree’s branching factor and affects its balance and performance.
- How does a B-T ree differ from a Red-Black Tree?
While both B-Trees and Red-Black Trees are balanced data structures, they differ in their internal organization and balancing mechanisms. B-Trees are optimized for disk storage and support multi-level indexing, whereas Red-Black Trees are primarily used for in-memory operations.
- Is a B-Tree always balanced?
Yes, by definition, a B-Tree is always balanced. It maintains a balanced structure through carefully orchestrated insertion and deletion operations, ensuring consistent performance for search and retrieval tasks.
- Can a B-Tree have duplicate keys?
Yes, a B-Tree can have duplicate keys. Unlike some other tree data structures like Binary Search Trees, B-Trees allow duplicate keys, which can be beneficial in certain applications.
- How is data insertion handled in a B-Tree?
During data insertion, a B-Tree ensures that the tree remains balanced by splitting nodes if necessary. This process involves redistributing keys among nodes to maintain the tree’s balance while accommodating new data.
- What happens during a deletion in a B-Tree?
When a node is deleted from a B-Tree, the tree undergoes restructuring to maintain its balanced nature. Depending on the deletion scenario, nodes may be merged or redistributed to ensure that the tree retains its efficiency.
Conclusion
B-trees are versatile data structures that offer efficient storage and retrieval capabilities, particularly in scenarios involving large datasets. Their balanced nature, coupled with logarithmic search complexity, makes them indispensable in database systems, file systems, and other applications where rapid data access is paramount.
